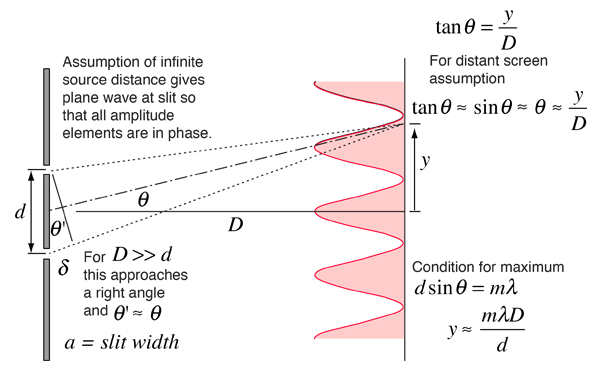
Double slit interference. Image from HyperPhysics.

Double slit interference. Image from HyperPhysics.
Bright regions occur at angles \(\theta\) for which$$\bbox[silver]{\sin\theta=\frac{m\lambda}{d},}$$ where \(d\) is the distance between two slits, \(\lambda\) is the wavelength, and \(m\) is the order number (see above image for detail).
Intensity of two-source interference follows $$I=I_0\cos^2\frac{\phi}{2},$$where \(I_0\) is the maximum possible total intensity, and \(\phi\) is the relative phase between two source. It can be shown that for the case of double slit interference, the phase difference \(\phi\) is \(2\pi d\sin\theta/\lambda\). Therefore, consider the effect of two-slit interference only, the intensity profile is$$\bbox[silver]{I(\theta)=I_0\cos^2\left(\frac{\pi d\sin\theta}{\lambda}\right).}$$
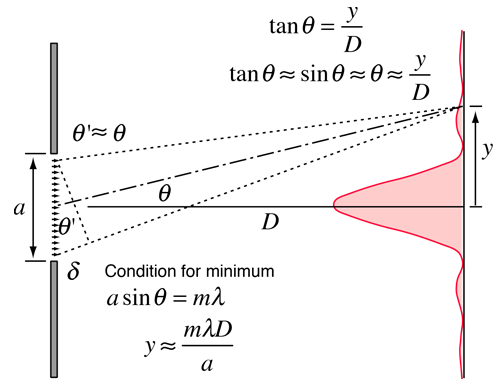
Single slit diffraction. Image from HyperPhysics.
Angles of minimum intensity are at$$\bbox[silver]{\sin\theta=\frac{m\lambda}{a},}$$ where \(a\) is the slit width, \(\lambda\) is the wavelength, and \(m\) is the order number.
Similarly, the intensity profile with the effect of single-slit diffraction only can be found to be$$\bbox[silver]{I=I_0\ \mathrm{sinc}^2\left(\frac{\pi a\sin\theta}{\lambda}\right)},$$ where the sinc function is defined as \(\mathrm{sinc\ }x=\sin x/x\) for \(x\neq 0\) and \(\mathrm{sinc\ }0=1\).
Interference can be used in studying crystal structure. X-rays are often used in a such case. Rays reflected from different layer of crystal gives the information about the crystal structure.
Bragg's law. Image from Wikipedia.
Constructive interference occurs at$$2d\sin\theta=m\lambda.$$
Verify the phase difference (a) for double slit interference is \(\pi d\sin\theta/\lambda\); (b) for single slit diffraction is \(\pi a\sin\theta/\lambda\).
(Hint: find the path difference first)