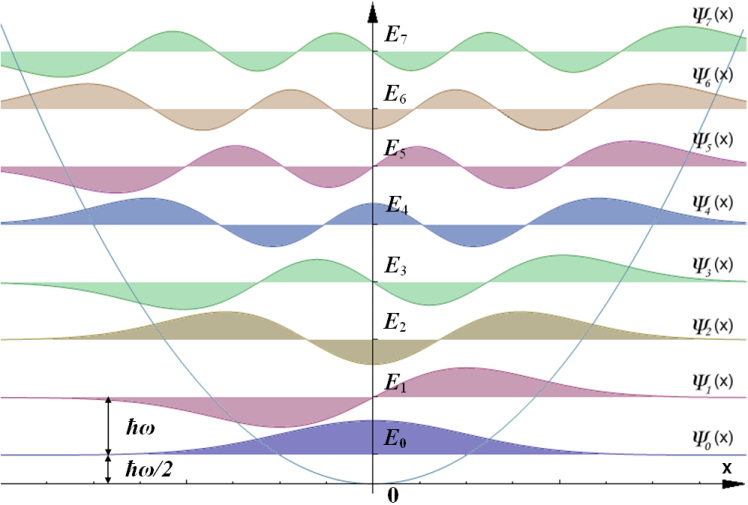
3.3 Case 3 The Simple Harmonic Oscillator

Let's consider the case of a simple harmonic oscillator.

For a spring-mass system, we have the potential energy $U(x)=1/2\kappa x^2$, where $\kappa$ is the spring constant. Insert the potential energy into the time-independent Schrödinger equation, we have

$$ -\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi(x)+\frac{1}{2}\kappa x^2\psi(x)=E\psi(x). $$

Solving this differential equation is beyond the scope of this series. However, we can still guess and check the simplest solution, a Gaussian. Actually, a Gaussian do satisfy the above differential equation. Start with $\psi(x)=A\exp(-ax^2)$, and plug back into the differential equation. The result is that $a=\sqrt{m\kappa}/2\hbar$. Then applying normalization condition gives $A=(m\kappa/\pi^2\hbar^2)^{1/8}$.

Actually this Gaussian is the first eigen equation $\psi_0(x)=(m\kappa/\pi^2\hbar^2)^{1/8}\exp(-(\sqrt{m\kappa}/2\hbar)x^2)$, and its corresponding eigen energy is $E_0=\hbar/2\sqrt{\kappa/m}$. It turned out that the complete eigen equations and eigen energies are

$$ \psi_n(x)=\frac{1}{\sqrt{2^nn!}}\left(\frac{m\omega_0}{\pi\hbar}\right)^{1/4}\exp(-m\omega_0x^2/2\hbar)H_n\left(\sqrt{\frac{m\omega_0}{\hbar}x}\right), $$

$$ E_n=\left(n+\frac{1}{2}\right)\hbar\omega_0. $$

Here $\omega_0=\sqrt{\kappa/m}$ is the natural frequency, and $H_n$ is the Hermite functions (physics) which is defined as

$$ H_n(z)=(-1)^n\mathrm{e}^{z^2}\frac{d^n}{dz^n}\left(\mathrm{e}^{-z^2}\right). $$

*Ladder Operator Method

Notice that the eigen energies are equally separated by $\hbar\omega_0$, Thus it is convenient to work in the energy basis, instead of using real space wave functions. Introducing the energy eigenstates $\ket{n}$, and define following operators:

$$ \begin{gather} a=\sqrt{\frac{m\omega}{2\hbar}}\left(\hat{x}+\frac{i}{m\omega}\hat{p}\right),\\ a^\dagger=\sqrt{\frac{m\omega}{2\hbar}}\left(\hat{x}-\frac{i}{m\omega}\hat{p}\right). \end{gather} $$

Here the subscription under $\omega$ is omitted for simplicity. Pay attention that here $\hat{x}$ and $\hat{p}$ are operators as well, and if were applied to wave functions, they could be expressed as $\hat{x}=x$, and $\hat{p}=-i\hbar\frac{\partial}{\partial x}$.

One can check the effect of applying $a$ or $a^\dagger$ to an eigen wave equation is to turn it into another eigen wave equation with eigen energy either increased or decreased by $\hbar\omega$ . Thus, in energy basis, we have

$$ \begin{gather} a^\dagger\ket{n}=\sqrt{n+1}\ket{n+1},\\ a\ket{n}=\sqrt{n}\ket{n-1}. \end{gather} $$

Notice that

$$ a^\dagger a\ket{n}=a^\dagger\sqrt{n}\ket{n-1}=n\ket{n}. $$

Therefore, we can define number operator as $N=a^\dagger a$. Then, the Hamiltonian can be expressed as

$$ H=\hbar\omega\left(a^\dagger a+\frac{1}{2}\right). $$